ベクトルを理解する
ベクトルには次元と方向があります。例: 次のイメージは、矢印として描かれたデカルト座標系の 2 次元ベクトル を示しています。
ベクトル の先頭は点 にあります。x 座標値は 、y 座標値は です。座標はベクトルの成分とも呼ばれます。
類似性
2 つのベクトルが類似しているかどうかを判断するには、いくつかの数式を使用できます。視覚化して理解するのに最も直観的なものの 1 つは、コサイン類似度です。3 セットのグラフを示す次のイメージを考えてみましょう。
最初の図のように、ベクトル と が互いに近くを指している場合、これらのベクトルは類似しているとみなされます。ベクトルは、互いに垂直を向いている場合は無関係とみなされ、ベクトルが互いに離れる方向を向いている場合は反対とみなされます。
それらの間の角度、 は、それらの類似性の適切な尺度です。角度 はどのように計算できますか ?
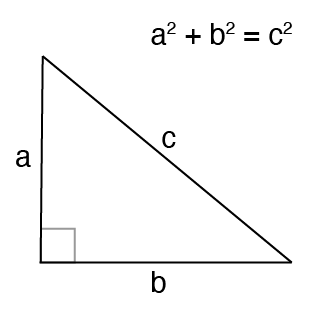
ピタゴラスの定理 [Wikipedia] (英語) は誰もがよく知っています。
a と b の間の角度が 90 度ではない場合はどうなるでしょうか？
余弦定理 [Wikipedia] (英語) の登場です。
次の図は、このアプローチをベクトル図で示しています。
このベクトルの大きさは、その成分に関して次のように定義されます。
2 つのベクトル と の間の内積は、その成分に関して次のように定義されます。
コサインの法則をベクトルの大きさと内積で書き直すと、次のようになります。
を に置き換えると、次のようになります。
これを展開する (英語) とコサイン類似度 [Wikipedia] (英語) の公式が得られます。
視覚化するのは難しいですが、この公式は 2 または 3 より高い次元でも機能します。ただし、ある程度は可視化することができます (英語) 。AI/ML アプリケーションのベクトルの次元は数百、さらには数千になるのが一般的です。
ベクトルの成分を使用した高次元の類似度関数を以下に示します。合計の数学的構文 [Wikipedia] (英語) を使用して、以前に与えられた振幅と内積の 2 次元定義を N 次元に拡張します。
これは、ベクトルストアの単純な実装で使用される重要な式であり、SimpleVectorStore 実装で見つけることができます。
